当前位置：首页 > 热点关注

广义相对论和弯曲时空是什么关系？坐标变换的时候基矢量和矢量分量会怎么变？11月24日12时，《张朝阳的物理课》第一百八十八期开播，搜狐创始人、董事局主席兼CEO、物理学博士张朝阳坐镇搜狐视频直播间，先定性地给网友们介绍了弯曲时空的概念，解释了惯性质量等于引力质量的重要性，然后以欧几里得空间为例，介绍了在一般坐标基下的矢量表示，最后推导了在坐标变换下坐标基之间的变换以及矢量分量之间的变换。

浅析时空与几何 探讨引力质量和惯性质量

在之前的物理直播课中，张朝阳介绍过矢量和坐标变换。简单来说，矢量是一个具体的东西，坐标只是描述手段。当采用另一个坐标时，矢量是不变的，但是坐标基矢改变了，因此矢量在新基矢下的分量也随之改变了。在欧几里得空间中，张朝阳用木棍作为矢量的类比。如果简单地采用直角坐标系的话，那么这个木棍的各个分量就是它到各个坐标轴的投影。

进一步地，如果将坐标系进行了旋转，但是木棍保持不动，那么木棍所代表的矢量保持不变。但是因为坐标系经过了旋转，坐标基矢已经改变了。同时，木棍在新坐标下上沿各个轴的投影也与旧坐标的不一样的，因此矢量分量也改变了。但是，不管采用什么坐标系，木棍的长度都是不变的，这就是矢量的不变量，它的值不依赖于坐标的选择。

如果给三维欧几里得空间加上时间轴，同时用狭义相对论中定义的时空间隔来作为这个四维空间上的“距离”的定义，这样就会得到闵氏空间。如果是在广义相对论的框架下讨论时空，那么这样的时空与闵氏时空最大的区别之一就是其中用来定义“距离”的不再是狭义相对论中的时空间隔，或者更准确地说，所用的度规不再是闵氏度规。

在时空中，事件用一个点表示，点的坐标包含了事件发生的时刻以及空间位置这些信息。网友们或多或少都在各种关于广义相对论的科普中学到过弯曲时空的概念。如果要理解弯曲时空，可以简单地从空间中的弯曲曲面来理解。在曲面上，很多关于欧几里得空间的度量都不成立了，需要重建描述方式，这个描述方式就是数学中的微分几何。

除了曲面，其实三维空间也可以是弯曲的，只不过因为人们习惯了三维空间，所以没法直接想象出弯曲的三维空间这件事。如果再增加一个空间维度成为四维空间，就可以像理解二维弯曲曲面那样来理解弯曲的三维空间了（需要注意的是，不是所有弯曲三维空间都可以等距嵌入到四维平直空间中）。

不过，不管维度多高，这些弯曲空间上的距离都是正数值，在一点无穷小的邻域上，勾股定理还是成立的，这样的弯曲空间几何被称为黎曼几何。但是，在广义相对论中，因为存在时间轴，在每一个时空点的无穷小邻域上，它是无限接近于闵氏时空而非欧氏空间的，因此，时空的“间隔”不必是正的，它也可以是负的，这样的几何一般被称为伪黎曼几何。

张朝阳还强调，提空间曲面这个例子还需要注意的是，不是所有曲面都代表弯曲空间。随后，张朝阳拿出一张白纸，将它卷曲了起来，并告诉网友们说，这张纸目前所代表的曲面并不是“弯曲空间”，它只是在三维空间上看起来是弯曲的，但是它内在并不是弯曲的，因为它原本就是平直的纸卷起来的，“卷”这个动作对应着一种等距变换，不会改变曲面的内禀性质。大家所熟知的球面就是一个“弯曲空间”，它在不被撕碎或者不产生褶皱的情况下是无法展开成一个平面的。

介绍完弯曲空间的概念，张朝阳向网友们提起了引力质量和惯性质量是相同的这一物理知识。惯性的物理意义和“懒惰度”很像，一个人越懒惰，就越难被拉动起来干活。同样，一个物体的惯性越大，它就越难被从静止拉到特定的运动状态。物体的惯性正比于它的质量，也就是正比于它所含的物质的多少。这一件事情是很容易理解的，因为物质越多，越需要更多的力才能在特定时间内到达特定的运动速度，这一切都非常符合人的直观理解。因此，用惯性或者用牛顿第二定律来衡量的质量，就被称为惯性质量。

另一个与质量有关的是引力。根据牛顿引力定律，两个相距为r、质量分别为m1、m2的质点，它们之间的万有引力大小为

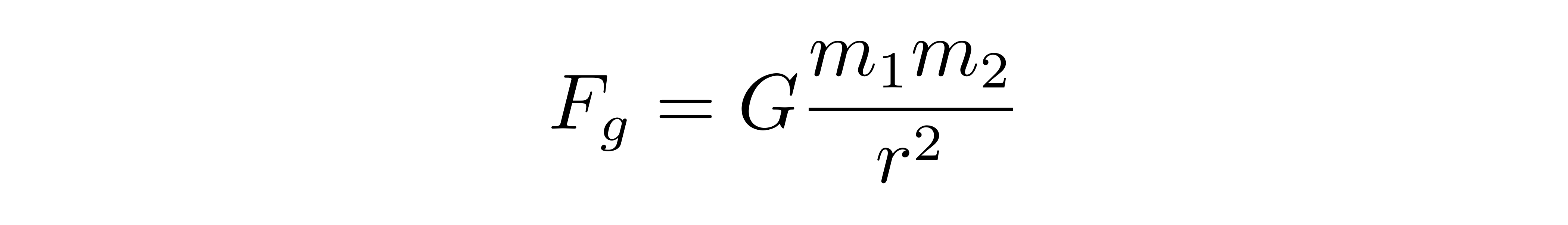
如果固定m2的质量，那么m1所受到的引力是正比于它的质量的。物理学家将引力所依赖的质量称为引力质量。

在目前的物理学中，惯性质量和引力质量是一样的，这是大家从中学接触万有引力开始就知道的一件事。但是它们为什么是一样的呢？这仅仅是巧合吗？可能有人会觉得这个问题很平凡，没有什么物理内涵。但是如果想一想电荷之间的库仑力，两个相距为r、电荷分别为q1、q2的质点，它们之间的库伦力大小为

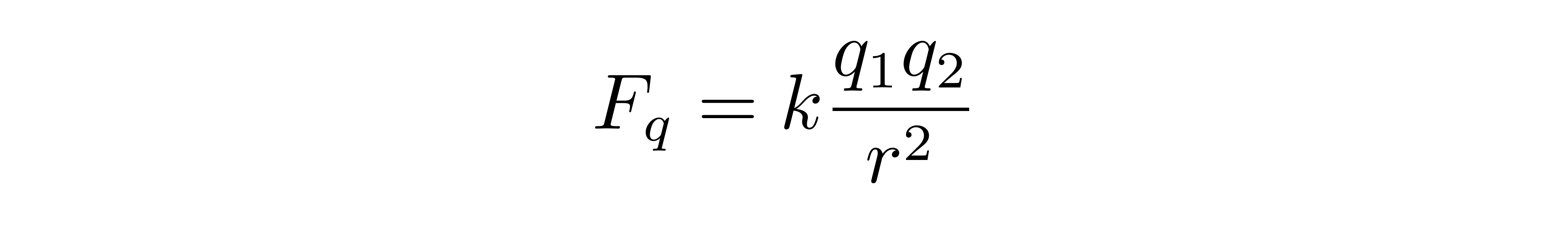
因此，也可以为引力定义一个类似于电荷的概念，比如将其称为“引力荷”，两个相距为r、引力荷分别为Q1、Q2的质点，它们之间的引力大小为

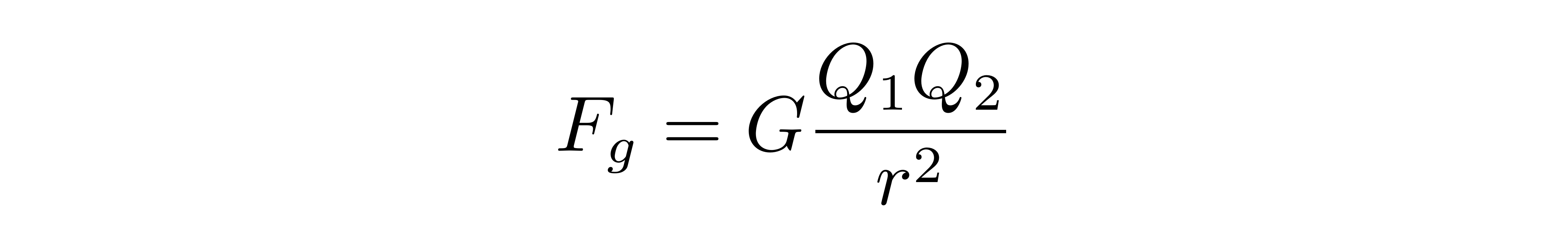
这样的话一切都没有问题，电荷是电荷，引力荷是引力荷，质量是质量，它们之间毫无关联。但是，牛顿告诉人们，这个所谓的引力荷，它就是质量——这相当于直接约化掉了一个物理量。那为什么“引力荷”就是质量呢？为什么电荷可以和质量毫无关系呢？这些迹象都表明，即使引力和库仑力都是反比于距离平方的，但是它们的本质很可能是不一样的。因此，“惯性质量与引力质量为什么是一样的？”这个问题至关重要，它所带来的物理内涵非常深远。

欧几里得空间下的基矢和坐标变换

为了能灵活处理广义相对论的弯曲时空，张朝阳以欧几里得平直空间为例介绍了张量、坐标变换等概念。张朝阳先介绍了张量的概念。以前介绍过的标量，其实就是零阶张量。而这里的矢量，是一阶张量。张量的阶数与空间维度无关，与它的指标数量有关。

张朝阳在以前的物理课介绍过二维空间旋转变换，因此他以这个作为切入点。考虑二维平面上的一个位置矢量

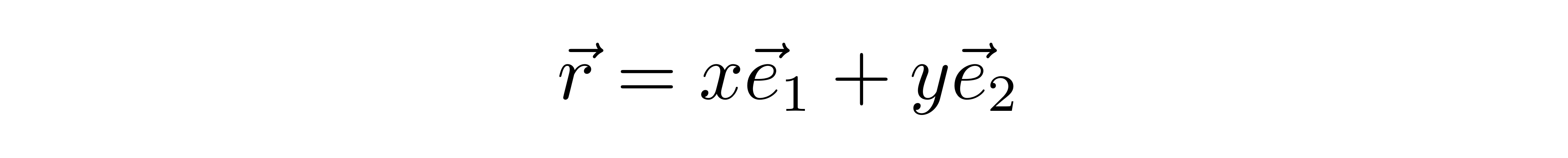
其中e1和e2是两个基矢，这里先假设它们是正交归一的。在之前的物理直播课中，张朝阳将这个矢量表示为列向量的形式：

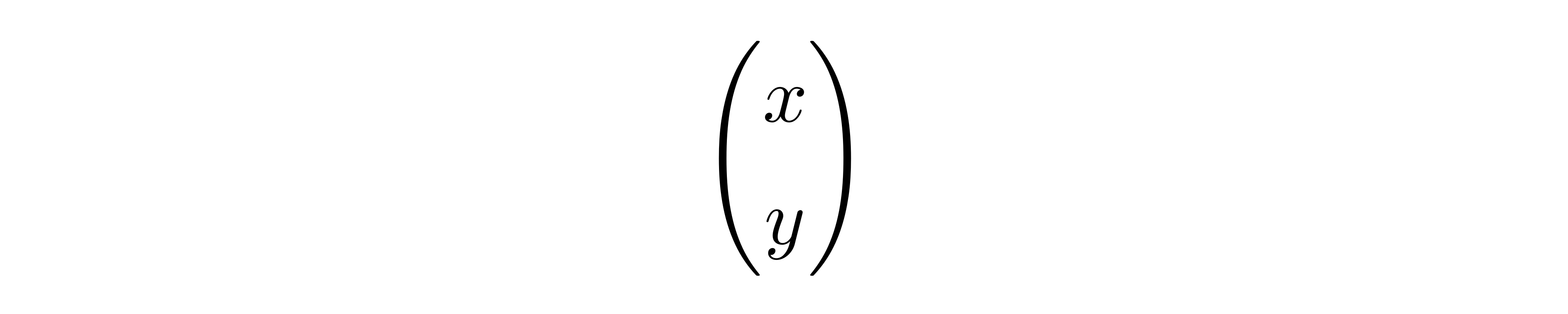
不过在这里，张朝阳使用了指标来表示。固定好基矢，用x^1表示矢量r的第一个分量，用x^2表示r的第二个分量：

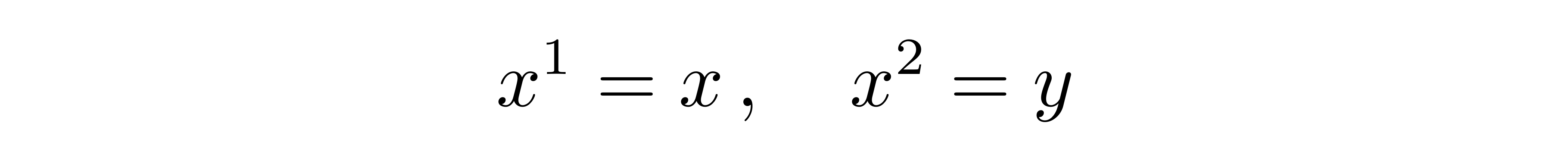
需要注意的是，处于“指数”位置的1和2不是代表次方，而仅代表指标的值。于是，矢量r可以被表示为

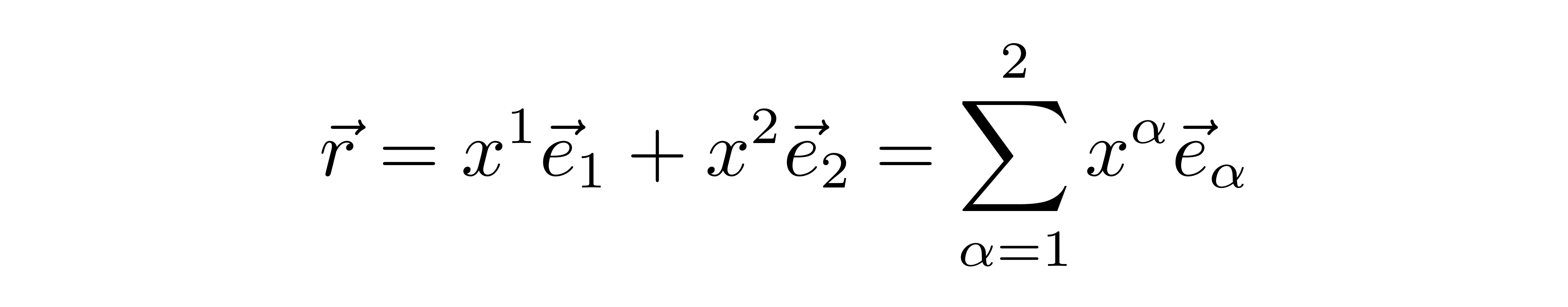
在相对论里边人们常使用爱因斯坦求和约定，当式子中出现一上一下的重复指标，就表示对指标进行求和。因此上式可以简写为

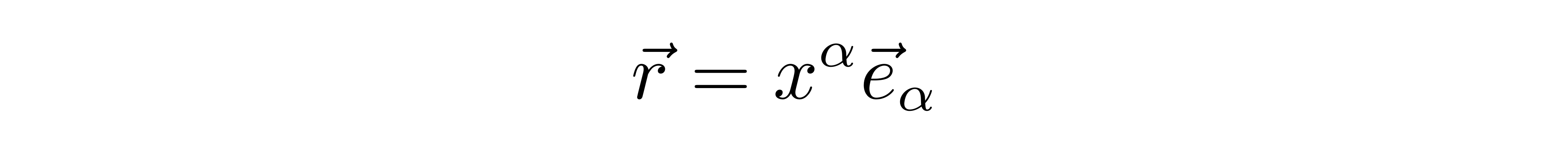
如果这时候采用了另一个坐标系，新坐标系与原坐标系仅仅相差了一个角度为ϕ的旋转。那么在此坐标变换下，有

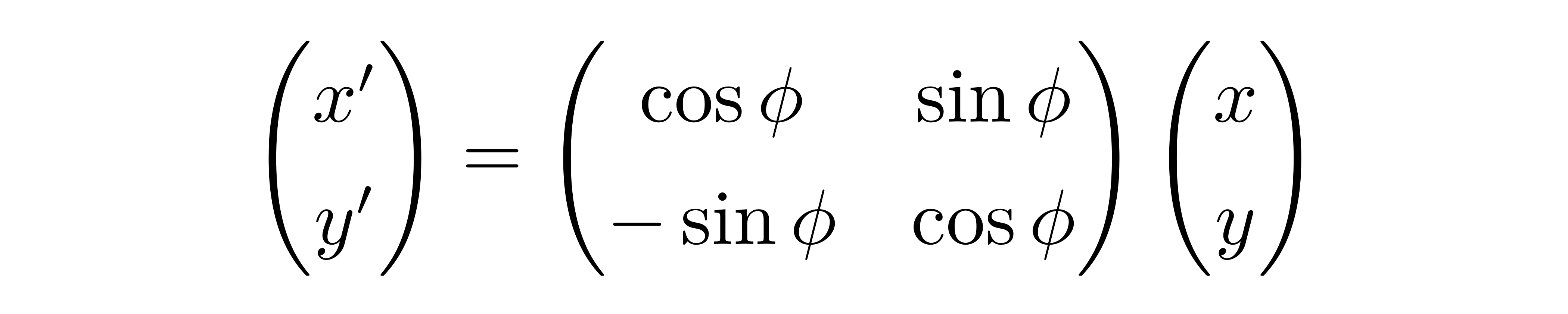
或者表示为

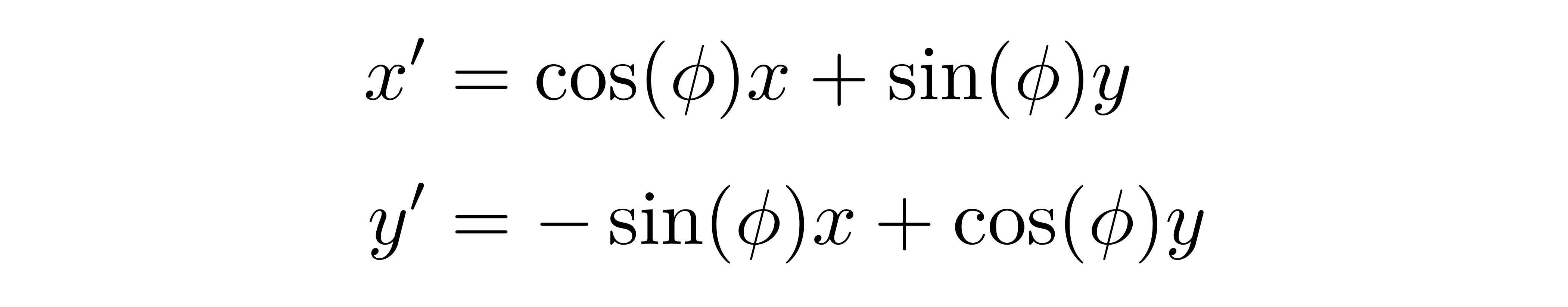
借助直角坐标的图，可得基矢之间的关系为

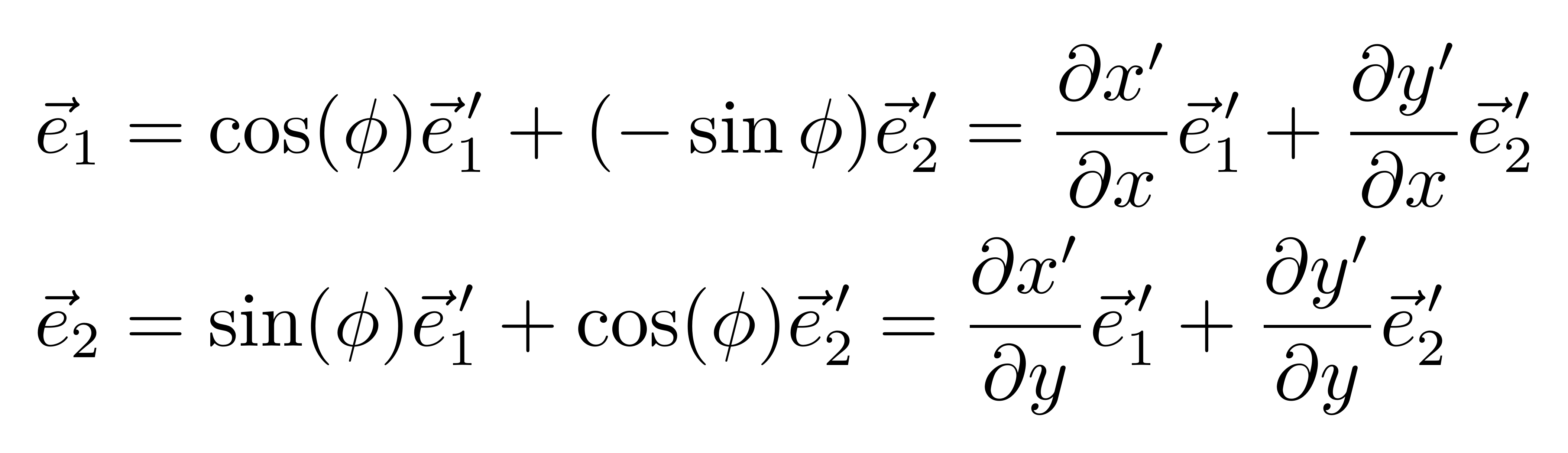
而上式最后的形式其实更通用，它不仅仅适用于这里介绍的旋转变换，它对任意的坐标变换都是适用的。借助爱因斯坦求和约定，上式可以被简写为

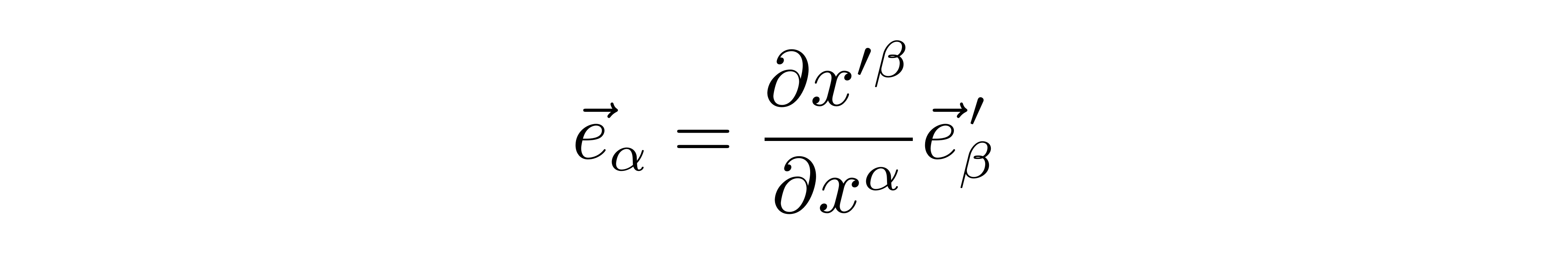
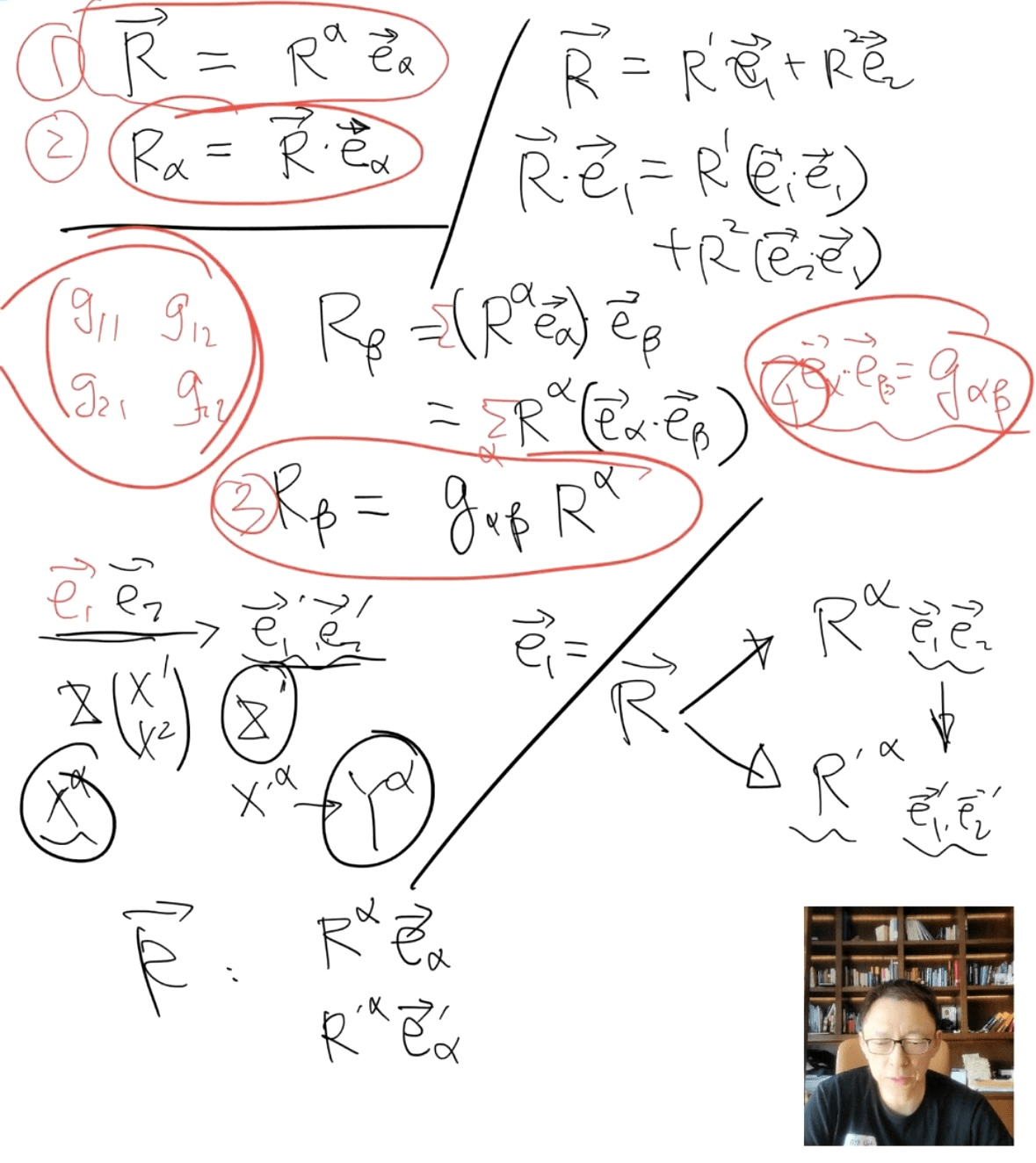
现在转向一般的坐标，对应的坐标基矢同样记为e1和e2，那么一般的矢量V依然可以表示为

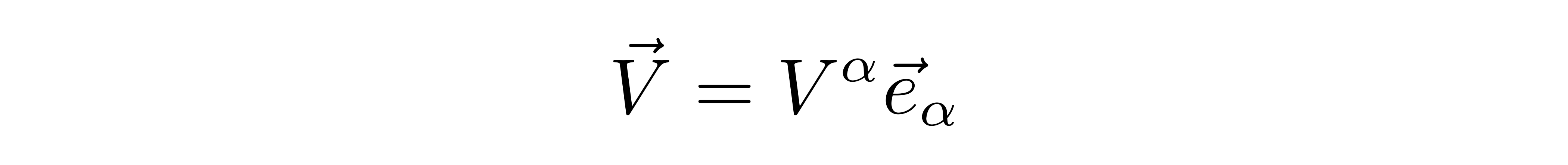
其中V^α可以被陈为逆变分量。另外，可以定义另一组分量为

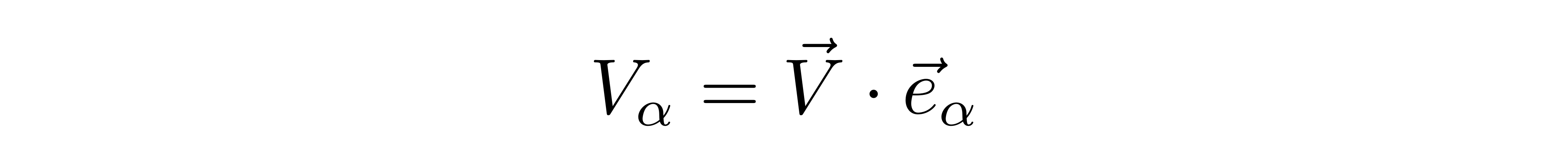
这组分量被称为协变分量。需要注意的是，因为这些基矢不必是正交归一的，因此一般不会有V_α=V^α，比如对于V_α，有

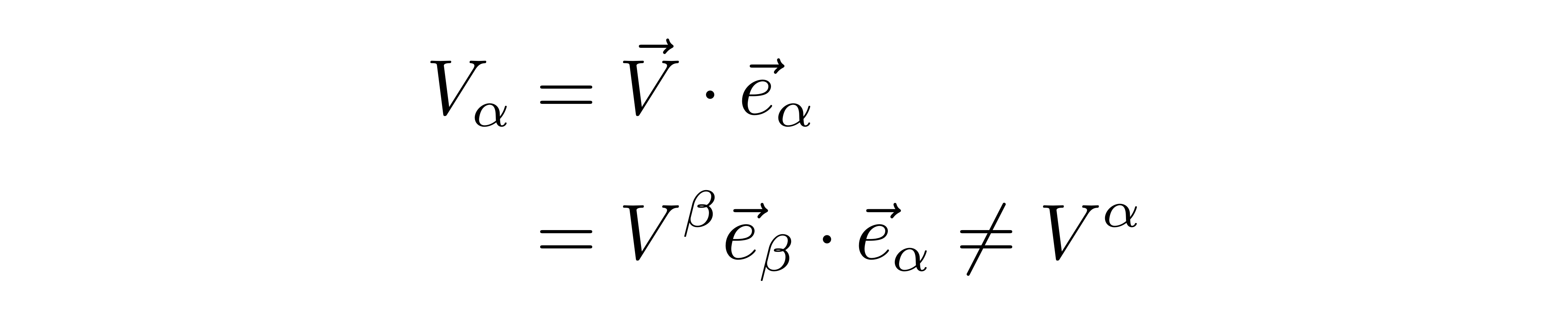
如果定义

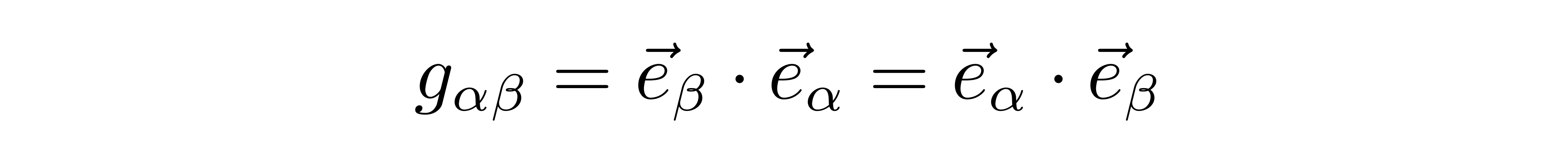
那么有

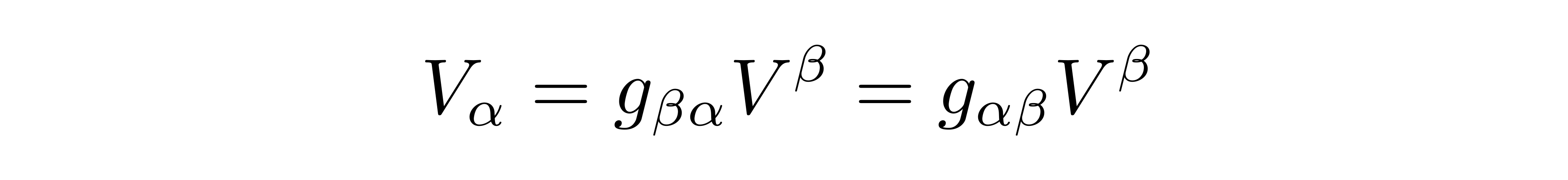
其实这里的g_{αβ}就是人们常说的度规。如果给定了度规和基矢，那么可以由矢量的逆变分量求出相应的协变分量。借助度规的可逆性，也可以由矢量的协变分量得到其逆变分量。因此，无论是协变分量还是逆变分量，都完整包含了这个矢量的所有信息。

（张朝阳介绍度规及协变分量的定义）

已知基矢在坐标变换下会怎么改变，那么矢量分量在坐标变换下会怎么变呢？这可以根据矢量的不变性来得到。在新老坐标系下分别有

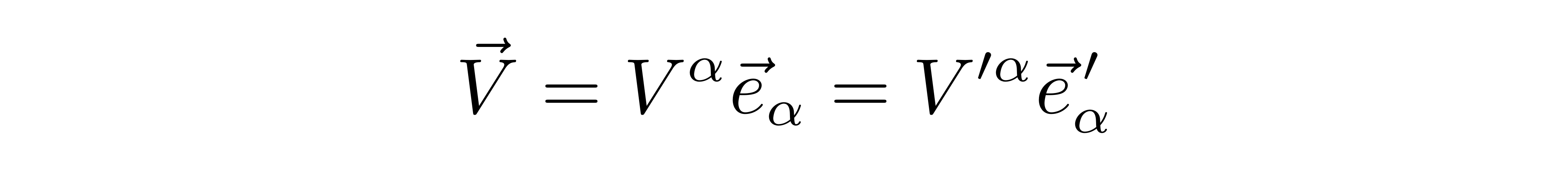
因为

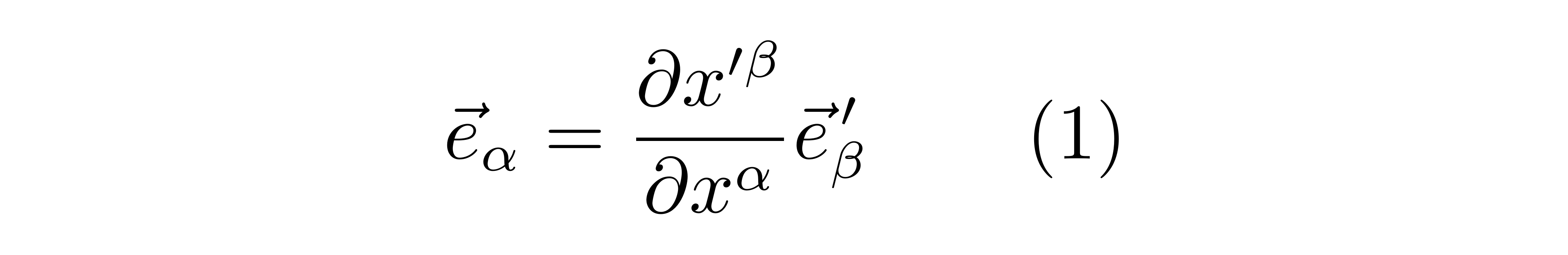
因此有

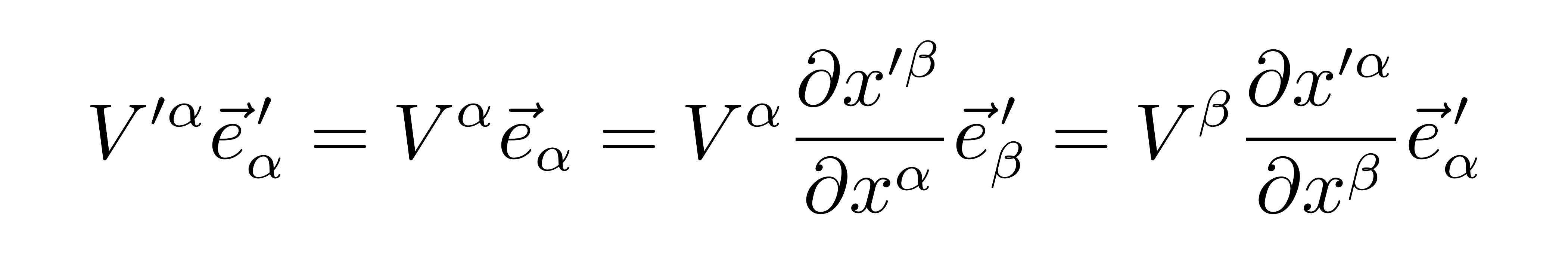
上式最后一个等号是因为求和指标的具体符号是不重要的，无论用α还是β又或者γ，只要是重复指标都表示对此指标进行求和，因此可以交换α和β指标。根据基矢展开的唯一性，可以得到

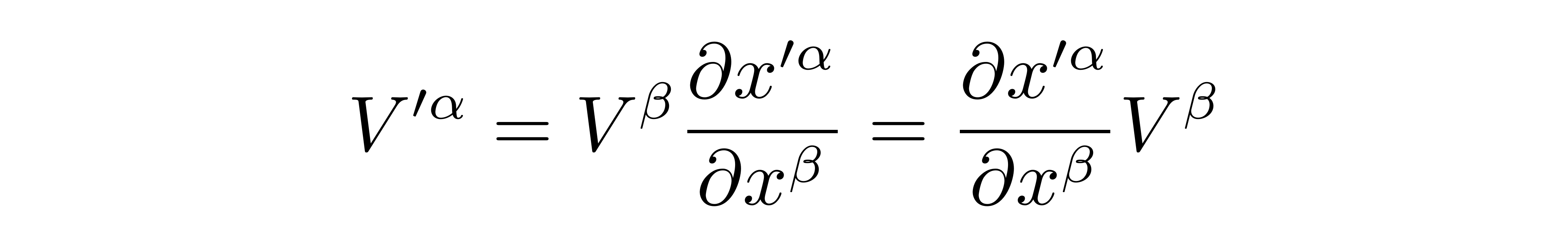
这就是逆变分量在坐标变换下的变换公式。对于协变分量，需要使用式(1)的逆变换公式：

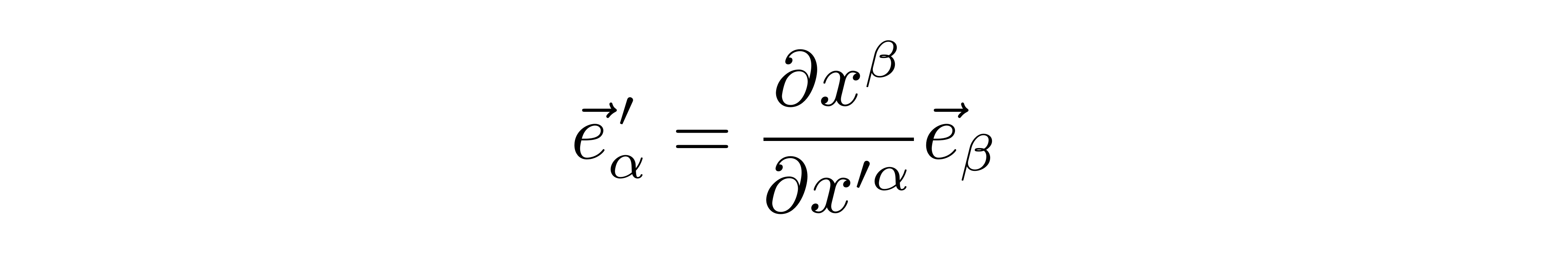
这个式子可以从两个角度来理解，第一个角度是借助变换矩阵的可逆性，其逆矩阵正好相当于将“分式”颠倒过来；第二个角度更好理解一些，就是考虑从带撇的坐标变换到不带撇的坐标，那么将这个变换套到式(1)即可得到上式。借助上式，可以得到

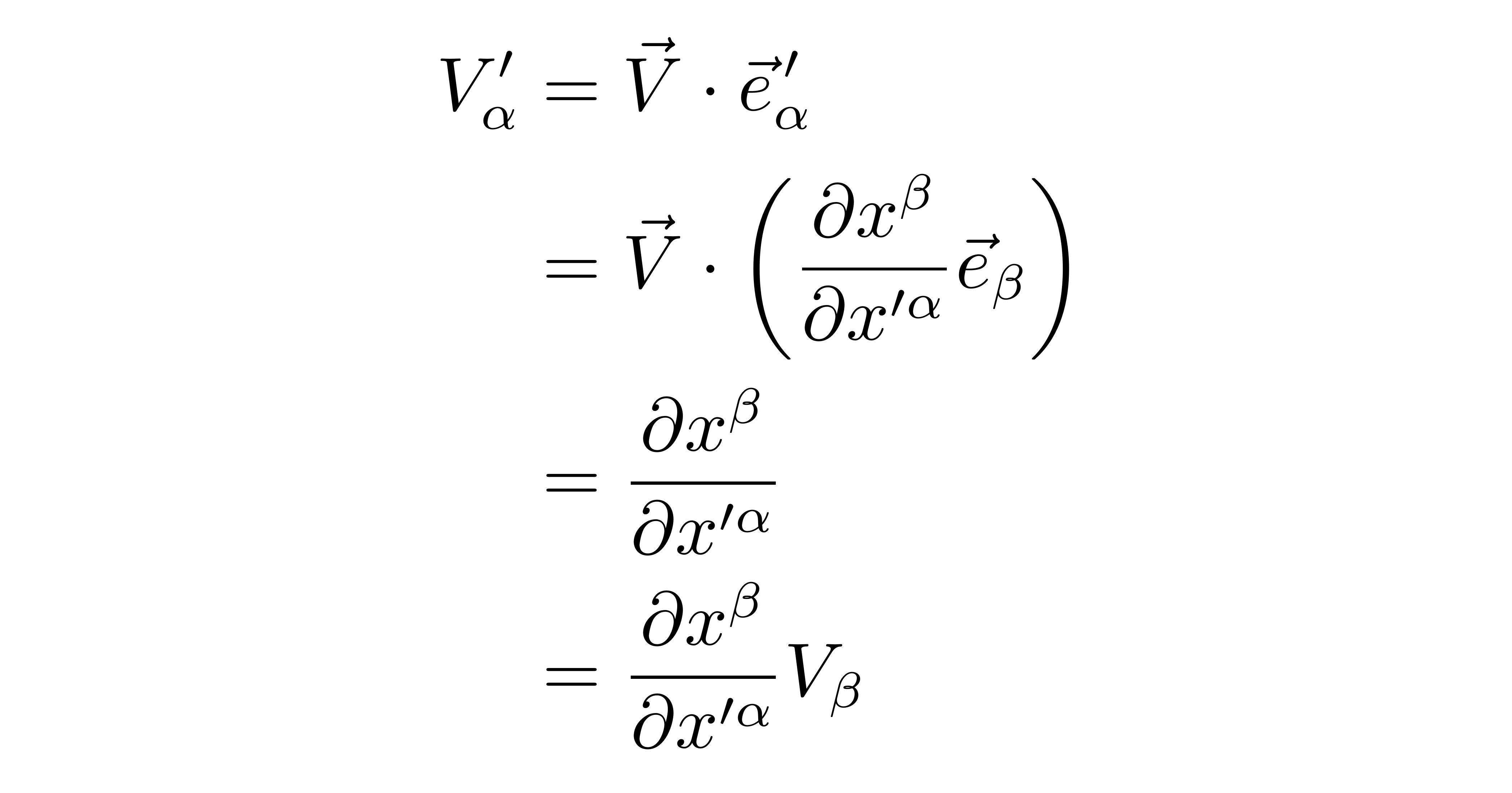
这就是协变分量在坐标变换下的变换公式。

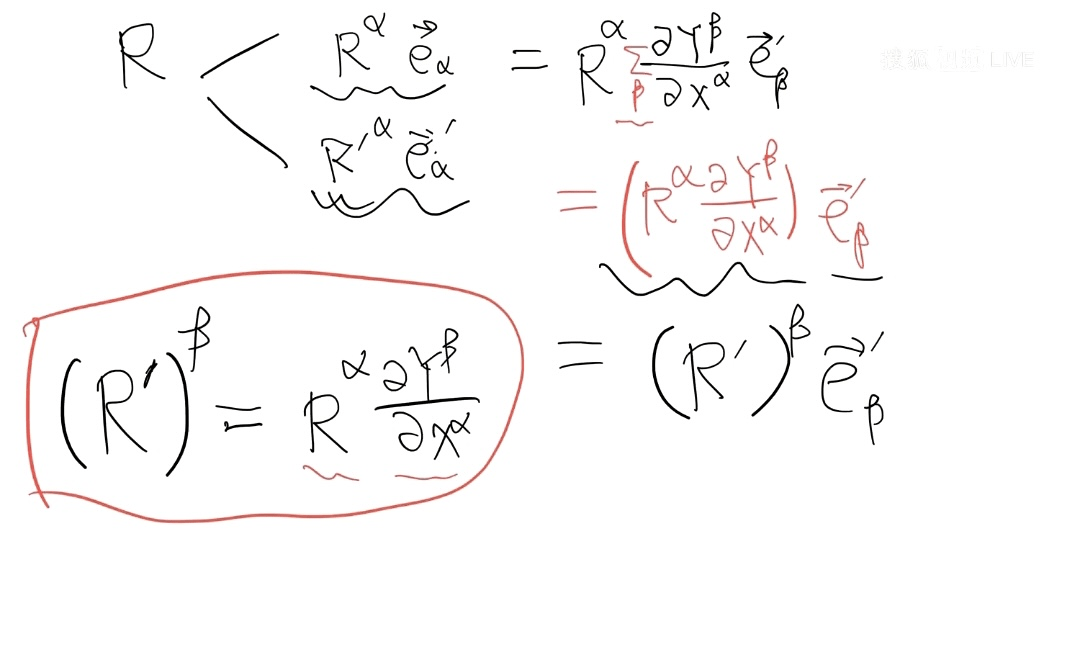（张朝阳介绍逆变分量在坐标变换下的变换公式）

据了解，《张朝阳的物理课》于每周五、周日中午12时在搜狐视频直播，网友可以在搜狐视频APP“关注流”中搜索“张朝阳”，观看直播及往期完整视频回放；关注“张朝阳的物理课”账号，查看课程中的“知识点”短视频；此外，还可以在搜狐新闻APP的“搜狐科技”账号上，阅览每期物理课程的详细文章。